はじめに
連続ウェーブレット変換(continuous wavelet transform : CWT)とは、時間周波数解析の一つであり、信号の時間ごとの周波数特性を見ることが出来ます。
今回はpythonでscipyやPyWaveletsといったライブラリではなく自作の連続ウェーブレット変換の関数を紹介します。また、実際にCWTを信号に対して行い、信号の特徴を抽出してみます。
連続ウェーブレット変換の概要、scipyやPyWaveletsライブラリを使用する方法については別途記事を書く予定です。
【世界で5万人が受講】実践 Python データサイエンス・オンライン講座
信号生成
次のようなsignal01とsignal02を作成し、連続ウェーブレット変換を行うための信号として用意しました。
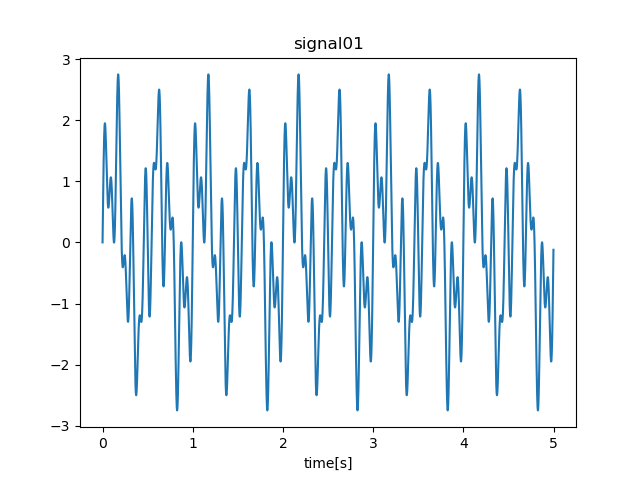
signal01
この信号は周波数2[Hz]、7[Hz]、13[Hz]の3つのsin波を合成したものになります。また、2[Hz]の信号の振幅が一番大きく、13[Hz]の信号の振幅が一番小さくなるようにしています。
合成前の3つの波形を見ると次のようになっています。
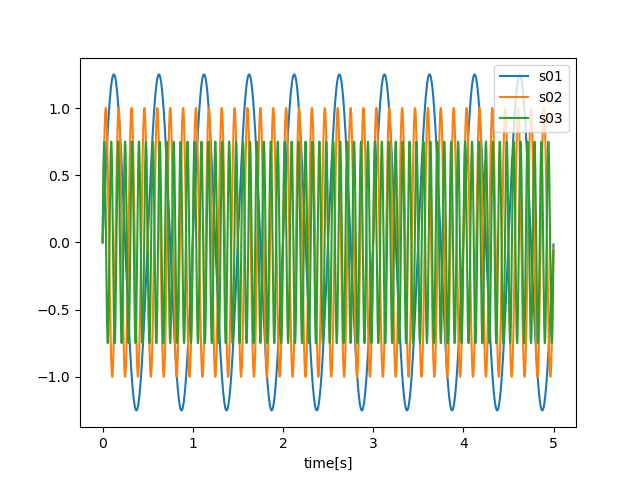
signal01は以下のプログラムで作成することができます。
|
1 2 3 4 5 6 7 8 9 10 11 |
Fs = 1000 # サンプリング周波数 Ts = 1 / Fs # 1ステップあたりの時間幅 time_S = 5 # 信号は5秒分 t_data = np.arange(0,time_S, Ts) # 5秒分の時間配列 f1, f2, f3 = 2, 7, 13 # 2[Hz], 7[Hz], 13[Hz]の信号 s01 = 1.25*np.sin(2*np.pi*f1*t_data) s02 = np.sin(2*np.pi*f2*t_data) s03 = 0.75*np.sin(2*np.pi*f3*t_data) signal01 = s01 + s02 + s03 # 3つの信号の合成信号 |
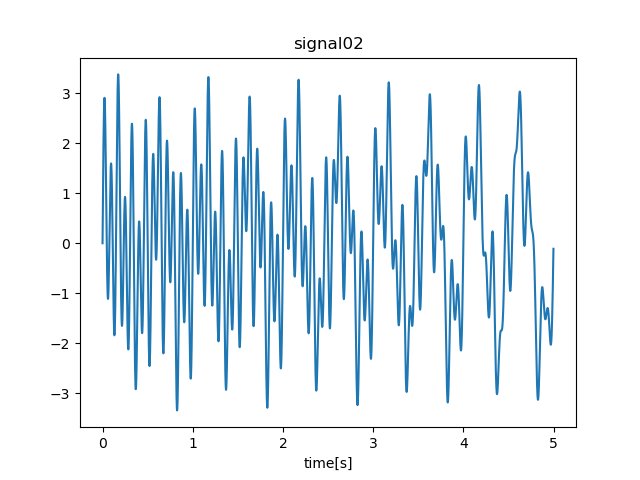
signal02
この信号は先ほどの信号と同じように周波数2[Hz]、7[Hz]、13[Hz]の3つのsin波を合成したものですが周波数2[Hz]の信号は時間ごとに減衰、13[Hz]の信号は時間ごとに増幅しています。
合成前の3つの波形を見ると次のようになっています。
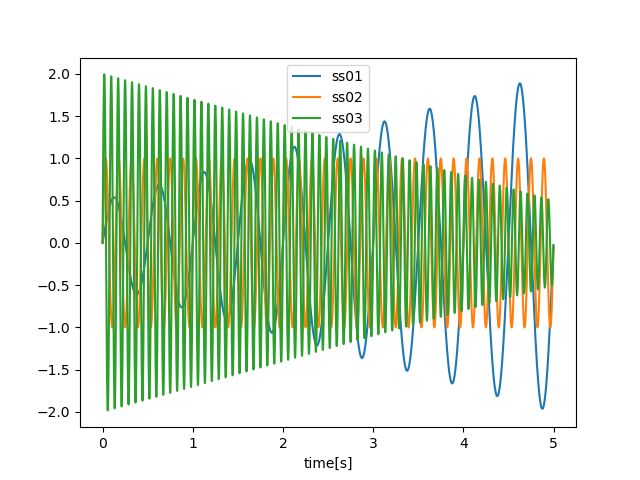
signal02は以下のプログラムで作成することができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Fs = 1000 # サンプリング周波数 Ts = 1 / Fs # 1ステップあたりの時間幅 time_S = 5 # 信号は5秒分 t_data = np.arange(0,time_S, Ts) # 5秒分の時間配列 f1, f2, f3 = 2, 7, 13 # 2[Hz], 7[Hz], 13[Hz]の信号 amp = np.linspace(0.5, 2, num = Fs* time_S) # 増幅用 ss01 = np.sin(2*np.pi*f1*t_data)* amp ss02 = np.sin(2*np.pi*f2*t_data) ss03 = np.sin(2*np.pi*f3*t_data)* np.flipud(amp) signal02 = ss01 + ss02 + ss03 # 3つの信号の合成信号 |
プログラム例
連続ウェーブレット変換を行うプログラムは以下の様になります。
マザーウェーブレットにはモルレーウェーブレットを採用しています。また、連続ウェーブレット変換によって、信号のパワースペクトル密度の時間、周波数ごとの変化を算出しています。今回は最大20[Hz]までのパワースペクトル密度を計算しました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 |
import numpy as np import matplotlib.pyplot as plt import math width = 6 # マザーウェーブレット:モルレーウェーブレット def morlet(x, f, width): sf = f / width st = 1 / (2 * math.pi * sf) A = 1 / (st * math.sqrt(2 * math.pi)) h = -np.power(x, 2) / (2 * st**2) co1 = 1j * 2 * math.pi * f * x return A * np.exp(co1) * np.exp(h) # 連続ウェーブレット変換 def mycwt(Fs, data, fmax, wavelet_R=2): # Fs: サンプリング周波数 # data: 信号 # wavelet_R: マザーウェーブレットの長さ(秒) # fmax: 解析する最大周波数 Ts = 1 / Fs # サンプリング時間幅 data_length = len(data) # 信号のサンプル数を取得 # マザーウェーブレットの範囲 wavelet_length = np.arange(-wavelet_R, wavelet_R, Ts) # 連続ウェーブレット変換後のデータを格納する配列の作成 wn = np.zeros([fmax, data_length]) # 連続ウェーブレット変換の実行 for i in range(0, fmax): wn[i,:] = np.abs(np.convolve(data, morlet(wavelet_length, i+1, width), mode='same')) wn[i,:] = (2 * wn[i, :] / Fs)**2 return wn # 連続ウェーブレット変換後のカラーマップ作成関数 def cwt_plot(CWT, sample_time, fmax, fig_title): plt.imshow(CWT, cmap='jet', aspect='auto',vmax=abs(CWT).max(), vmin=-abs(CWT).max()) plt.title(fig_title) plt.xlabel("time[ms]") plt.ylabel("frequency[Hz]") plt.axis([0, len(sample_time), 0, fmax-1]) plt.colorbar() if __name__ == "__main__": # 信号作成 ---------------------------------------- Fs = 1000 # サンプリング周波数 Ts = 1 / Fs # 1ステップあたりの時間幅 time_S = 5 # 信号は5秒分 t_data = np.arange(0,time_S, Ts) # 5秒分の時間配列 f1, f2, f3 = 2, 7, 13 # 2[Hz], 7[Hz], 13[Hz]の信号 # signal01作成 ---------------------------------------- s01 = 1.25*np.sin(2*np.pi*f1*t_data) s02 = np.sin(2*np.pi*f2*t_data) s03 = 0.75*np.sin(2*np.pi*f3*t_data) signal01 = s01 + s02 + s03 # 3つの信号の合成信号 # signal02作成 ---------------------------------------- amp = np.linspace(0.5, 2, num = Fs* time_S) # 増幅用 ss01 = np.sin(2*np.pi*f1*t_data)* amp ss02 = np.sin(2*np.pi*f2*t_data) ss03 = np.sin(2*np.pi*f3*t_data)* np.flipud(amp) signal02 = ss01 + ss02 + ss03 # 3つの信号の合成信号 # 連続ウェーブレット変換 ---------------------------------------- fmax=20 # 解析する最大周波数 cwt_signal01 = mycwt(Fs=Fs, data=signal01, fmax=fmax) cwt_signal02 = mycwt(Fs=Fs, data=signal02, fmax=fmax) # 以下、図用 ---------------------------------------- plt.figure(1) # s01, s02, s03の図 plt.plot(t_data[:], s01, label="s01") plt.plot(t_data, s02, label="s02") plt.plot(t_data, s03, label="s03") plt.legend() plt.xlabel("time[s]") plt.figure(2) # signal01の図 plt.title("signal01") plt.plot(t_data, signal01) plt.xlabel("time[s]") plt.figure(3) # ss01, ss02, ss03の図 plt.plot(t_data, ss01, label="ss01") plt.plot(t_data, ss02, label="ss02") plt.plot(t_data, ss03, label="ss03") plt.legend() plt.xlabel("time[s]") plt.figure(4) # signal02の図 plt.title("signal02") plt.plot(t_data, signal02) plt.xlabel("time[s]") plt.figure(5) # signal01を連続ウェーブレット変換した時のカラーマップの図 fig_title01 = "cwt signal01" cwt_plot(cwt_signal01, t_data, fmax, fig_title01) plt.figure(6) # signal02を連続ウェーブレット変換した時のカラーマップの図 fig_title02 = "cwt signal02" cwt_plot(cwt_signal02, t_data, fmax, fig_title02) plt.show() |
実行結果
以下にsignal01とsignal02を連続ウェーブレット変換した結果を示します。
ここで縦軸の目盛が0[Hz]から始まっていますが表記上の問題であり、本来の値は縦軸の目盛に1を足したものです。注意してください。また、図の色は信号のパワースペクトル密度を表しています。
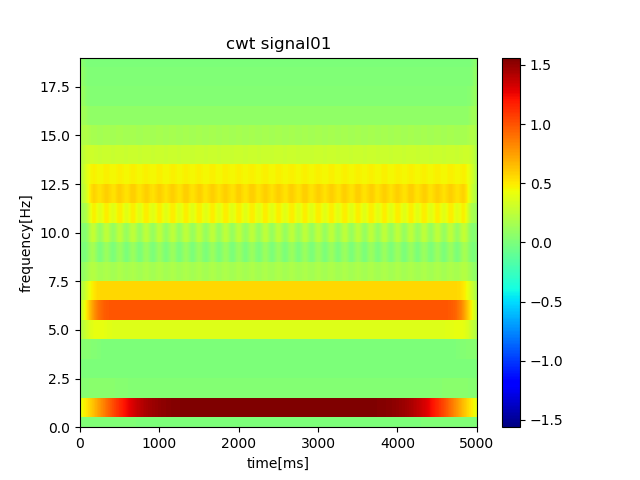
signal01の結果
結果の図より、2[Hz]、7[Hz]、13[Hz]付近のパワースペクトル密度が大きくなっているのが分かります。またそのパワースペクトル密度は2[Hz]が最も大きく、13[Hz]が最も小さくなっています。
また連続ウェーブレット変換の特徴から、「周波数が低いほど周波数分解能が高いが時間分解能は低い」ということと、「周波数が高いほど周波数分解能は低いが、時間分解能は高い」ということが分かります。
signal02の結果
結果の図より、2[Hz]、7[Hz]、13[Hz]付近のパワースペクトル密度が大きくなっているのが分かります。
さらにsignal02の特徴の通り、2[Hz]の信号は前半のパワースペクトル密度が大きく、後半は小さい、13[Hz]はその逆で7[Hz]は一定になっています。
時間ごとの変化が非常に分かりやすくなっています。

最後に
以上が、pythonで連続ウェーブレット変換を自作する方法と、2つの信号を例に実際に解析を行った結果になっています。
時間周波数解析を行うことで、信号の時間ごとの周波数特性を視覚的に分かりやすくできるので是非、利用してみてください。




コメント
pythonを勉強中の大学生です。
現在ウェーブレット変換を使いたいと思っているのですが、
「縦軸の目盛が0[Hz]から始まっていますが表記上の問題であり、本来の値は縦軸の目盛に1を足したものです。」
という点で、これは現在サイトに載っているコードを改正することで解決可能でしょうか?
> これは現在サイトに載っているコードを改正することで解決可能でしょうか?
はい、軸の表示を変更していただければ解決可能です。